Paxlovid and Immortal Time

Experts are often unscrupulous

Today’s post will be short, this is another example of how study design allows people to arrive at their desired outcome. Last night I came across a tweet about a recent study on the use of Nirmatrelvir(Paxlovid)-ritonavir in outpatients in the state of Colorado. More on the study details soon. This was the tweet:

I looked at the axes and kept scrolling. The reason is that we’re dealing with rare events. I want to briefly make a point about the scale and avoid getting bogged down and confusing myself, so let’s keep it simple:

Note: Tangent incoming, scroll down to skip.

Studies allow us to calculate things like risk in different groups. In a prospective study you might find two groups that differ in some way you think will affect some outcome. If you track these groups over time you can then say things about the risk of said outcome. That risk can be expressed in terms of absolute risk and relative risk.

Retrospective studies are easier to do because you can just look back at data that already exists. The trouble is you can’t technically calculate relative risk, because you started with the outcome. So you use something else called an odds ratio and the idea is if the outcome is rare enough, the odds ratio will approximate relative risk and be useful. To avoid getting really boring let’s use the concept of relative and absolute risk.

Take two examples:

1. There is a hypothetical infection that kills 50% of infected people. Let’s imagine you make a drug to treat it and run an RCT to test the efficacy of said drug. This is a 2,000 person study, half get your drug, the other half get placebo. In the placebo arm 500 people die, as expected. In the treatment arm 250 people die.

   1. Absolute risk reduction is 0.25, or 25%. Put simply, this drug reduced the death rate by 25%, from 50%.

   2. Relative risk reduction is 0.5, or 50%. The risk of death was reduced by one half.

2. Now we have a new hypothetical infection that kills 0.4% of infected people. Same setup as before for sample size. This time in the placebo arm 4 people die, but in the treatment arm only 2 people die.

   1. Absolute risk reduction is 0.002, or 0.2%. This drug saved two lives.

   2. Relative risk reduction is 0.5, or 50%. The risk of death was reduced by one half.

This is why you have to know the overall risk in order to interpret how much benefit is being derived from an intervention. In the first scenario the drug saved 250 lives, versus just 2 in the second scenario. The relative risk reductions were identical, because that calculation is relative, as advertised. I mentioned odds ratios approximate relative risk, but only when the event is rare. So the odds ratio by definition is only used in the context in which relative risks requires scrutiny.

Before we talk through the main topic for this post, let’s just look at what the absolute risk reductions would have been if this were a prospective study.

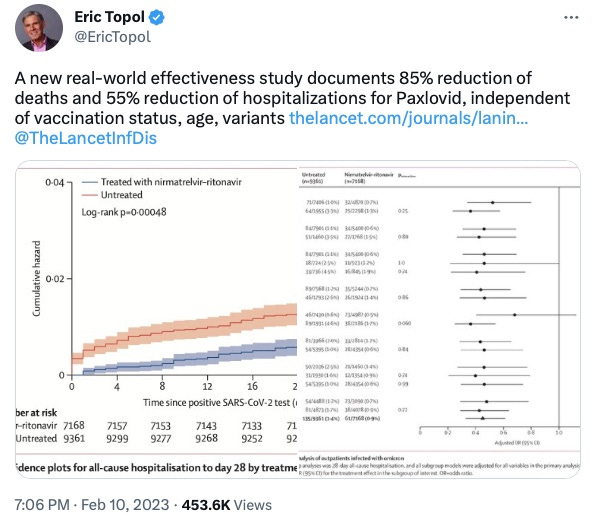
• Death (All-cause 28 day mortality): 2/7,168 patients treated with Paxlovid died. 15/9,361 patients untreated died. This would give us an ARR of 0.0013, or 0.13%.

• Hospitalization (All-cause 28 day hospitalization): Hospitalization rates were 61/7,168 for Paxlovid, 135/9,361 for untreated. This would give us an ARR of 0.0059, or 0.59%.

Hospitalization is bad and death is worse— I am not arguing that these reductions are inherently meaningless. I just want to remind people that the less common an event is, the more misleading the RRR becomes.

Note: Tangent Over

Back to last night: So I looked at the numbers in that tweet, internally groaned about relative risk vs. absolute risk, and scrolled on. I then saw multiple other tweets criticizing the study Dr. Topol had shared, emphasizing the difference in hospitalization rates at the beginning of the study.

Basics about this study: Here is the link

The researchers wanted to see how well Paxlovid is working in the real world, so they used retrospective data from Colorado, over a roughly 6 month period (March-September 2022). Paxlovid is used to reduce the risk of hospitalization or death in patients with Covid. The idea is if you get covid, and you take Paxlovid early after infection, it will be less severe.

They compared the 28-day hospitalization rate in people who had either received Paxlovid or not. Now about the difference at the start of the study:

I have zoomed in on a portion of the graph showing hospitalizations at day zero. You can scroll back up to the first tweet I showed or find the graph in the paper itself. What we see here is that there is a big difference at day 0 between the untreated (red line) and treated (blue line) groups. That’s fishy, as it is hard to imagine Paxlovid’s mechanism of action is to teleport patients out of the hospital, especially in a study that assesses its use in the outpatient setting. I don’t recommend checking twitter at the end of a long day, as I was tired and a little irritable. So I responded to Dr. Topol with this:

That was pretty immature of me, as it reads as snarky, which I don’t aspire to be. Anyways, you live and you learn, stay off twitter when you’re tired. But then earlier today I saw another tweet from Dr. Topol responding to some of the criticism of the study:

I’ll readily admit that I had not read the paper, but this made me interested. It’s also generally bad form to not read a paper before criticizing it, but I was comfortable doing so because a difference at baseline tells you that the data is inherently skewed. How in the world might they explain their way out of a large difference at day 0? Let’s start with the groups:

Paxlovid group: They found patients that were prescribed Paxlovid in the outpatient setting. They ran into a problem because most of those patients didn’t have a positive covid test documented in the system. So they decided that they would subtract one day from the date of the prescription to approximate the time of the positive test. Originally they planned to subtract two days, but apparently for the patients they did have positive covid test data on a bunch of them were getting Paxlovid the same day or one day after, so they moved it up. This was an outpatient study, so they removed any patients given Paxlovid while in the hospital.

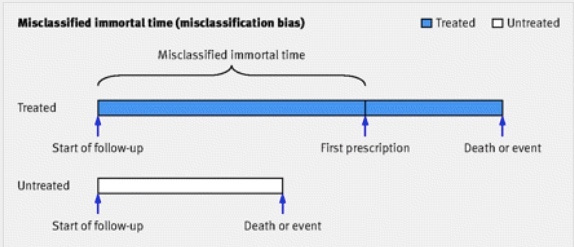
We already have a big problem. The outcome is hospitalization, and the intervention is prescription with Paxlovid. They didn’t have data on when the positive tests actually happened, so they subtracted a day. That means by definition from day 0-1 there will be no hospitalizations in the Paxlovid arm. This is an example of what is called “immortal time bias”, conveniently depicted below:

Using this figure as a guide, Paxlovid prescription is the first prescription, and the chunk of time before it is the time they conjured from thin air, in which by definition the patients were not at risk of hospitalization. Immortal time is by favorite bias because it sounds cool. In the first day of this study the treatment group (Paxlovid) was immortal! They could not be hospitalized, because the researchers made it so.

Control Group: The real kicker here I’ll just quote from the paper, which I have now officially read:

“We retained patients who were hospitalised or died later on the same day as their observed SARS-CoV-2 positive test, temporally after their first positive test given the common use of home self-testing during the study period.”

In other words, if you tested positive with covid and were hospitalized or died that day, you qualify for a control group to assess the efficacy of outpatient treatment. They try to justify this by assuming they had already tested positive at home. A glance at the graph makes it look like at least 30 patients were hospitalized on the day of their positive Covid test. The authors are having their cake and eating it too: immortal time for treatment group, same day hospitalizations counts for thee(control) but not for me(paxlovid).

There are plenty of other points to be made showing how these two groups are clearly different, but this is already longer than I planned, so I’ll conclude with one last weird thing in the protocol. The original protocol, which is in supplement 2, says “We will no longer be excluding patients who had a SARS-CoV-2+ test the same day as their hospitalisation, and will only be excluding patients who were already in the hospital when they received a positive test.” I just find this odd because the language clearly sounds like an amendment to the protocol, and not the original. There are other interesting changes they made, the most unfortunate of which in my mind is they decided not to compare Paxlovid to other treatments, as they had planned. Maybe they just weren’t powered for that.

Final Thoughts: I’m not sure how anyone can really defend this study. I guess the reasoning could be something like, “they explained why they added the immortal time and included same-day hospitalization in the treatment arm so it doesn’t matter”. But that’s obviously wrong. Maybe someone will explain what I’m missing here— my impression is this is a poor study and that was obvious at first glance. The real take home is don’t check twitter when you’re tired.